Day 7 - 梯度下降法

評估誤差

在前一天，我們討論了梯度下降法的主要目標是讓誤差最小化。那麼，誤差應該如何評估呢？

假設有很多個樣本 ( x, y )，我們需要計算模型預測的值 ŷ 與真實值y之間的差距。將所有樣本的誤差加總並取平均值，即可得出整體誤差。但誤差不能有負號，因此有兩種常見的方法來計算誤差：

1. 平均絕對誤差 (Mean Absolute Error, MAE)：使用誤差的絕對值來避免負號。
   
2. 均方誤差 (Mean Squared Error, MSE)：使用誤差的平方。
   

學習方式

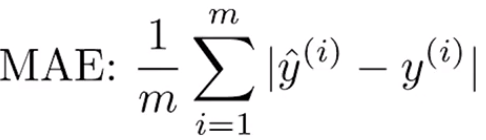
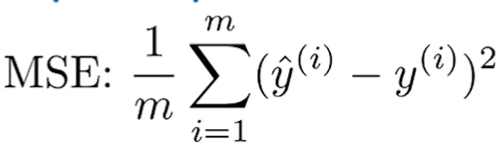
整個學習的目標是找到一組參數 ⊖，使得無論是平均絕對誤差還是均方誤差都接近於 0。這樣就可以精確地讓所有訓練樣本的輸出等於真實的輸出。

梯度下降法是一種迭代式的方法，透過反覆計算相同的步驟，逐漸得到最佳結果。其原理如下：

1. 初始猜測：隨意猜測一組參數 ⊖。
2. 誤差計算：根據目前的參數⊖計算誤差。
3. 參數更新：根據誤差的梯度計算出新的參數⊖。
4. 重複迭代：反覆上述步驟，直到誤差達到最小。

實際計算方式

每一組參數 ⊖對應一個誤差，因此誤差也是一個與⊖有關的函數，稱為J(⊖)。假設J函數有一個最低點，我們的目標是找到這個最低點。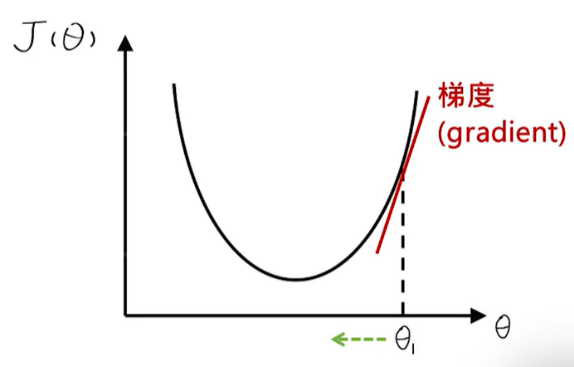

其步驟如下：

1. 任意猜測一組 ⊖。
2. 計算梯度：找到誤差函數J的梯度。
3. 更新參數：根據梯度值，更新⊖。
4. 重複步驟 2 和 3：直到梯度夠小為止。

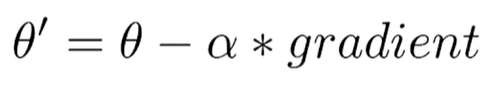
特別需要注意的是學習率 α。它是機器學習中需要調整的值。如果α 太大，可能會一次跨過終點，甚至增加誤差。反之，若α太小，學習效率會過低。通常，α的值會設在 0 到 1 之間。

多重局部最小值問題

現實情況中，誤差函數 J(⊖) 可能有多個局部最小值。梯度下降法只能找到相對極小值，而非絕對最小值。為了找到更好的⊖，可以使用多種不同的初始 ⊖。

詳細的梯度計算

前述步驟中，最關鍵的是梯度的計算。梯度就是誤差函數的偏導數。首先，使用⊖假設出函數，對每一個 ⊖進行偏微分。然後，將猜測的⊖帶入即可得到梯度。

對於數學基礎較弱的人來說，微分可能會較為困難。在此推薦參考 [深度學習講中文] 中對梯度下降法的簡單解釋，非常容易理解。